• Explore
• My scripts
• Calculator

Magic Draw

A small program based on maths equations, which shows you who draws equations in different forms, each one prettier than the next.
To add your own representation, add it to the ‘_list’ list in the form: (“x calcul”, “y calcul”).
There are two variables to use: p and i.

Examples of equations

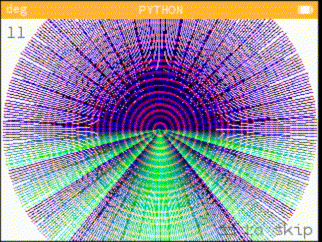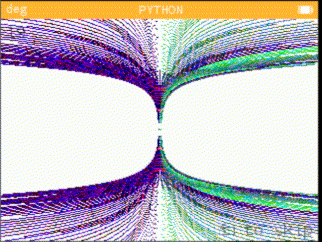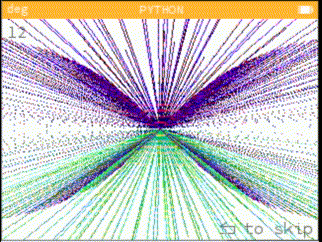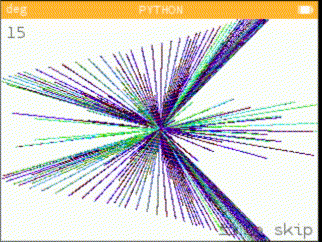
from math import *
from kandinsky import *
from time import *
 
def draw(index, loop, clear):
  if clear: fill_rect(0, 0, 350, 250, (255,255,255))
  draw_string(str(1+(len(_list)+index if index < 0 else index)), 5, 5, (100,100,100))
  draw_string("<", 219, 200, (100,100,100))
  fill_rect(220, 215, 15, 1, (100,100,100))
  fill_rect(235, 216, 1, -7, (100,100,100))
  fill_rect(236, 208, -15, 1, (100,100,100))
  draw_string("to skip", 245, 202, (100,100,100))
  exec("""for p in range({}):
    for i in range(496): 
      try: set_pixel(160+round({}), 110+round({}), {})
      except (OverflowError, ZeroDivisionError, ValueError):
        continue
      except KeyboardInterrupt: raise RuntimeError
      except: raise
  """.format(loop, _list[index][0], _list[index][1],
    "(cos(p)*1000, sin(i)*1000, log10(i-p)*1000)" \
      if _list[index][2] == True else "(0, 0, 0)"))

def start():
  x, loop = input("""{} equations found in the list.
Let empty to run all.
|-> """.format(len(_list))), input("""
Let empty for default value.
Loop: """)
  loop = 400 if loop == '' else int(loop)
  r = range(len(_list)) if x == '' else range(int(x)-1, int(x))

  for ii in r:
    time = monotonic()
    try: draw(ii, loop, 1)
    except (SyntaxError, IndexError): raise
    except:
      try: draw(ii, 1, 0)
      except: pass
    print("Drawn", ii+1, "in", int(monotonic()-time), "s")
  draw_string("End", 5, 5, (100,100,100))
     
_list=[
#           for x         |           for y           | color?
  ("cos(i)*111/(cos(p)+1)", "sin(i)*111/(sin(p)+1)"   , 1), #1
  ("cos(i)*111+p"         , "sin(i)*111+p"            , 1), #2
  ("cos(i)*111/(tan(p)+1)", "sin(i)*111/(sin(p)+1)"   , 1), #3
  ("cos(i)*111/(tan(p)+1)", "tan(i)*111/(sin(p))"     , 1), #4
  ("cos(i)*111/(1-cos(p)+1)", "sin(i)*111/(-sin(p)+1)", 1), #5
  ("cos(i)*111/(cos(p)+1)", "sin(i)/(sin(p)+1)"       , 1), #6
  ("cos(i)*111/(cos(p)+1)", "sin(i)*111/cos(p)**2"    , 1), #7
  ("cos(i)*111/(cos(p)+1)", "sin(i)*111/(cos(p)**2+1)", 1), #8
  ("cos(i)*111/(cos(p)+1)", "sin(i)*130/(tan(tan(p)))", 1), #9
  ("tan(tan(i))*111/sin(p)", "tan(i)*111/cos(sin(p))" , 1), #10
  ("cos(i)*p"             , "sin(i)*p"                , 1), #11
  ("tan(tan(i))*p"        , "sin(i)*p"                , 1), #12  
  ("cos(p)*i"             , "tan(p)*i"                , 0), #13
  ("tan(tan(tan(i)))/tan(p)", "tan(i)*p/sin(p)"       , 1), #14
  ("cos(tan(i))*p"        , "cos(i)*p"                , 1), #15
  ("sin(i)*p*cos(sin(i))" , "sin(p)*111/cos(tan(i))"  , 1), #16
  ("cos(p)*i*tan(cos(p))-111", "cos(i)*p/tan(i)"      , 1), #17
  ("sin(cos(tan(p)))*i"   , "tan(i)*p"                , 1), #18
  ("exp(abs(log(p)))*sin(i)", "log(p)/cos(i)*10"      , 1), #19
  ("exp(abs(log(p,i)))*64*sin(i)", "log(p)/cos(i)*5"  , 1), #20
  ("exp(abs(log(p)))*sin(i)", "sin(i)*50/sin(p)"      , 1), #21
  ("cos(p)*50/(sin(i)+1)" , "abs(p)/cos(i)"           , 1), #22
  ("asinh(p)/cos(i)"      , "cos(p)*111*sin(i)"       , 1), #23
  ("acosh(p)*111/(tan(i)+1)", "cos(p)*150/asinh(i)"   , 1), #24
  ("trunc(i)/cos(p)"      , "acosh(i)/-sin(p)"        , 0), #25
  ("cos(i)*50/(tan(p)+1)" , "acosh(i)*5/-tan(p)"      , 1), #26
  ("cos(i)*50/(tan(p)+1)" , "sin(i)*50/(cos(p))"      , 1), #27
]

start()