Construction d'une hypocycloïde
Trajectoire d’un point fixé à un cercle qui roule sans glisser sur un autre cercle dit directeur et à l’intérieur de celui-ci.

Autres courbes ici
>> go(7,2) (un tour ne suffit pas à tout afficher)
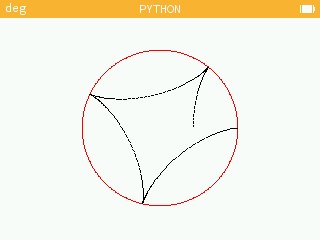
>> go(7,2,2) (on fait faire 2 tour au petit cercle. Mathématiquement, il faut chercher le plus petit multiple commun entre 7 et 2, à savoir 14, et diviser ce nombre par le premier paramètre (7) d’où 14/7 = 2 tours)
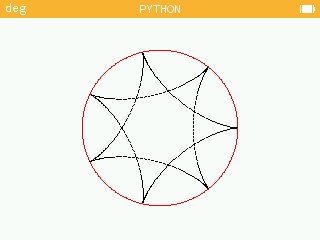
from kandinsky import * from math import * from random import * def go(r1,r2,t=1,n=500): p = 100/(r1+r2) for k in range(t*n): a = k/n*2*pi x = 160 + r1*p*cos(a) y = 110 + r1*p*sin(a) set_pixel(int(x),int(y),color(255,0,0)) x += r2*p*cos(a*(r1-r2)/r2) - r2*p*cos(a) y -= r2*p*sin(a*(r1-r2)/r2) + r2*p*sin(a) set_pixel(int(x),int(y),color(0,0,0)) while random()>.001: a=0