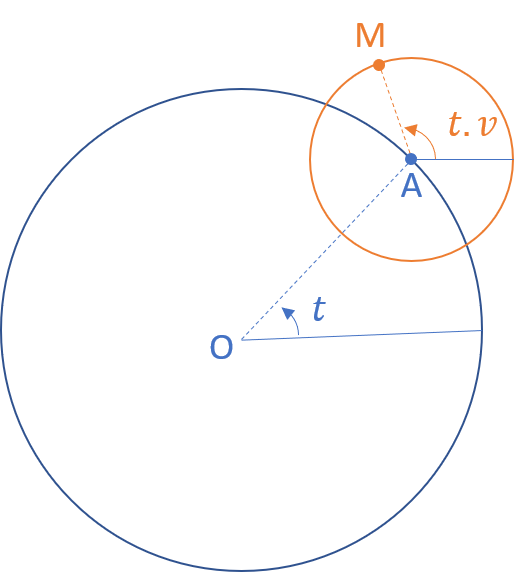
Un point A parcourt un cercle de rayon R1 (repéré avec un angle t).
Sur un second cercle de rayon R2 centré en A, on place le point M à l’angle t*v où v est fixé dès le départ.
Le programme ci-dessous affiche la trajectoire du point M
Il ne s’agit donc pas du cas d’un cercle roulant à l’intérieur (hypocycloïde) ou à l’extérieur (épicycloïde) d’un autre cercle comme on l’a sur les jeux pour enfants :

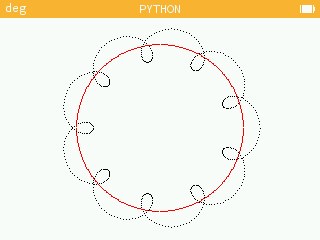
>> go(5,1,10) pour un grand cercle R1=5, un petit cercle R2=1 et une vitesse = 10 (le point M tourne 10 fois plus vite autour du petit cercle que le point A autour du grand)
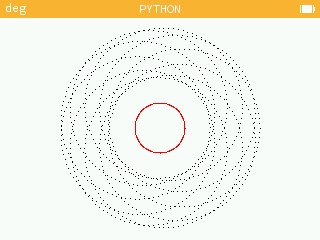
>> go(1,3,10,1000) pour un petit cercle R1=1, un grand cercle R2=3, une vitesse = 10 et 1000 points
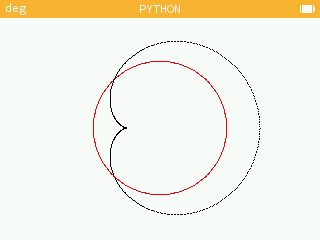
>> go(4,2,2) Le point M sur le petit cercle va 2 fois plus vite que le A sur le grand cercle
>> go(1,10,2)
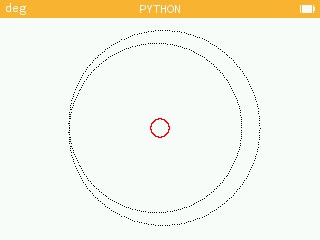
>> go(10,1,40,1000)
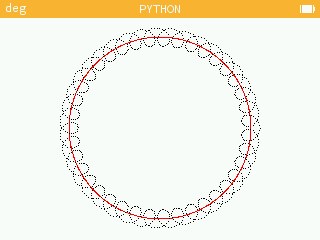
La ligne while random()>.001: t=0 est juste là pour ralentir la machine qui va trop vite pour afficher le déroulement…
from kandinsky import * from math import * from random import * # rayons cercles + vitesse cercle 2 + nb pts def go(r1,r2,v=1,n=500): p = 100/(r1+r2) for k in range(n): a = k/n*2*pi x = 160 + r1*p*cos(a) y = 110 + r1*p*sin(a) set_pixel(int(x),int(y),63488) set_pixel(int(x + r2*p*cos(a*v)),int(y + r2*p*sin(a*v)),0) while random()>.001: a=0