Renne dessiné avec des morceaux de paraboles.
La fonction coeff permet de trouver les coefficients a,b,c de la parabole passant par le sommet S(xs,ys) et le point A(x1,y1).
La fonction parab trace la parabole passant par S et A pour les abscisses entre x1 et x1 + d (d pouvant être négatif)
Il suffit donc de repérer (avec un logiciel comme Gimp) les coordonnées de S et A ainsi que la distance d, en faisant attention au fait que le centre de l’écran a pour coordonnées (0,0). Si l’image Gimp fait 320x220 pixels, il faudra effectuer les translations X - 160 et 110 - Y pour passer aux coordonnées de la tortue.
Ci-dessous le visuel expliquant d’où vient par exemple le parabole(0,-100,-45,-12,90) dans le script :
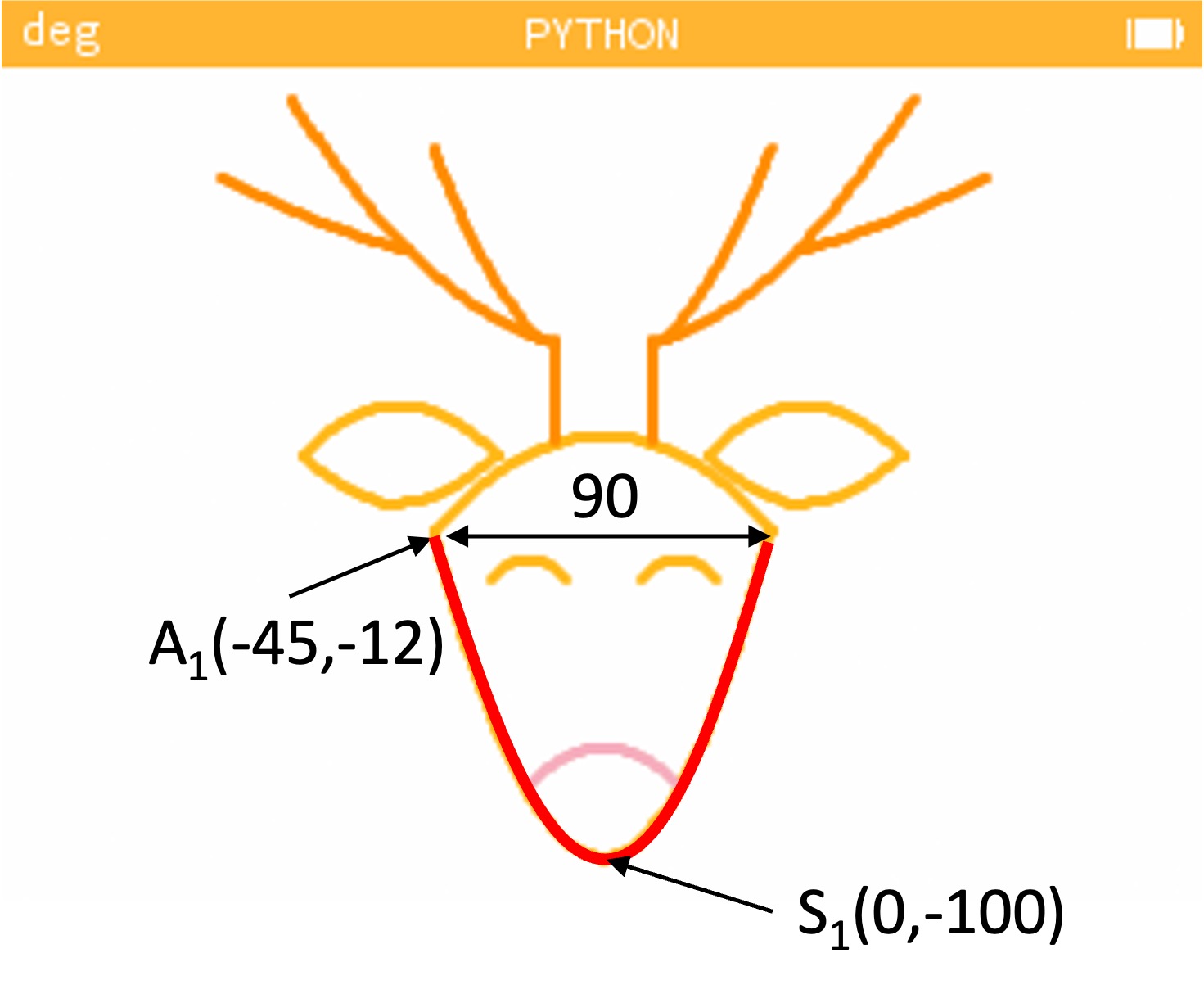
Ma chaine Youtube Schraf - Maths info
from turtle import * hideturtle() speed(1) def coeff(xs,ys,x1,y1): d = (x1 - xs) ** 2 a = (y1 - ys) / d b = - 2 * xs * a c = y1 - a * x1 ** 2 - b * x1 return [a,b,c] def point(x,a,b,c): goto(x, a * x * x + b * x + c) def parab(xs,ys,x1,y1,d): [a,b,c] = coeff(xs,ys,x1,y1) penup() point(x1,a,b,c) pendown() for k in range(11): point(x1 + d * k / 10, a, b, c) def verticale(x,y,d): penup() goto(x,y) pendown() goto(x,y - d) pensize(5) color(254,187,28) # tete parab(0,-100,-45,-12,90) parab(0,13,-45,-12,90) # oreilles + yeux for k in [-1,1]: parab(54 * k,21,54 * k - 26,8,52) parab(54 * k,-5,54 * k - 26,8,52) parab(20 * k,-20,20 * k - 10,-25,20) # bouche color(247,175,184) parab(0,-70,-20,-80,40) # bois color(254,141,3) for k in [-1,1]: parab(0,36,83 * k,103,-70 * k) parab(0,55,102 * k,82,-50 * k) parab(0,30,45 * k,90,-28 * k) verticale(13 * k,40,28) color(255,0,0) penup() goto(0,-55) pendown() circle(4)