Il s’agit ici d’adapter pour la NUMWORKS le programme écrit initialement en BASIC dans la revue MICR’ORIC de 1983 pour l’ordinateur Oric.


Observez le temps d’exécution sur votre calculatrice par rapport à celui annoncé dans la revue…
Exemple de graphique (avec une version légèrement améliorée) pour f(z) = 70*cos(z*z/100)*exp(-z*z/1000) :

f(z) = 20*sqrt(exp(-sin(z/3))) :

f(z) = 110*cos(z/30)*sqrt(exp(-sin(z/3))) :
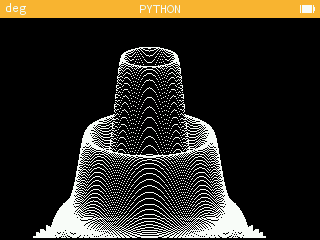
Le chapeau :

Ce que vous pouvez modifier dans le script :
- la valeur de m initialement mise à 30 comme dans la revue peut être augmentée.
- au lieu de r=y1 vous pouvez aussi mettre r=60 (et -60 plus loin) pour que la base du graphique ne soit plus un disque mais un carré (mais le visuel est alors moins fun !)
- Le .7 de la ligne 31 permet d’avoir une vue plus ou moins plongeante (testez avec 0.1 et 1 par exemple)
- L’astuce pour ne pas voir les parties cachées de la surface est, pour un x donné, de n’afficher le pixel que si la valeur du y est supérieur au max des valeurs précédentes (par exemple si les valeurs de y sont 3, 5, 9, 6, 15, 11, 13, 18 et 2, les valeurs réellement affichées seront 3,5,9,15 (car le 6 est <9), 18 (car 11 et 13<15) et 18.
from math import * from kandinsky import * # Testez avec go(f1), go(f2) etc. def f1(z): return 110*exp(-z*z/300) def f2(z): return 90*cos(z*z/70)*exp(-z*z/400) def f3(z): return 90-z*z/10 def f4(z): return 90*cos(z*z/35)*exp(-z*z/600) def f5(z): return 80*cos(z/20)*sqrt(exp(-sin(z/3))) # go(f6,1.9) def f6(z): return 40*sqrt(exp(-sin(z/1.5))) def go(f,v=.7): fill_rect(0,0,320,222,(0,0,0)) x,m = 10,30 q=-m while q<m: y1=sqrt(m*m-q*q) q+=m/150 l=-m r=y1 while r>=-y1: r-=0.5 s=f(sqrt(q*q+r*r))-v*r if s>l: l = s set_pixel(int(x),150-int(l),(255,255,255)) x+=1