• Explore
• My scripts
• Calculator

Vidéo d’explications

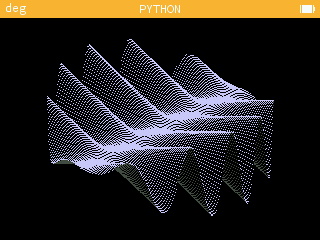
Résumé de la vidéo

• On parcourt tous les pixels (i,j) de l'écran de la machine de la gauche vers la droite et de bas en haut
• On transforme les coordonnées du pixel (i,j) de l'écran en coordonnées (x,y)dans le plan qui est en vue isométrique
• Si le point (x,y) est dans le rectangle défini par les bornes Xmax et Ymax, on cherche le z = f(x,y)
• On regarde alors si le point doit être tracé ou s'il est caché, cela dépend des points qui ont été tracés précédemment pour la même abscisse i. Si le z est plus grand que le maximum déjà à l'écran ou s'il est plus petit que le minimum déjà à l'écran, on peut afficher le point (ce qui actualise le minimum et maximum), sinon on ne fait rien.

Modifications possibles

Une modification très sympathique du programme concerne la ligne :

if abs(x) <= xmax and abs(y) <= ymax:

qui permet de savoir si le point est dans le rectangle défini par Xmax et Ymax. On peut en effet ne garder que les points qui sont dans l'ellipse définie par Xmax et Ymax. Vous remplacez la ligne par :

if (x / xmax)**2 + (y / ymax)**2 <= 1:

Une autre modification simple et impressionnante est de mettre la partie inférieure de la surface en une couleur plus foncée (comme si l'éclairage provenait du dessus). Il suffit pour cela de mettre une couleur sombre (17000 par exemple) lorsque z <= n et une couleur claire (52831 par exemple) sinon.

Le programme ci-dessous propose la version améliorée.

Quelques idées

Le plus amusant est bien entendu d'inventer les équations et de regarder ce que cela donne !

Attention, si vous faites des division

---

from math import *
from kandinsky import *

def f0(x,y): return 5*x*sin(5*y)
def f1(x,y): return 10*sin(4*x)*y
def f2(x,y): return 90*cos(x*x+y*y)*exp(-(x*x+y*y)/5)
def f3(x,y): return -400/exp(x*x+y*y)
def f4(x,y): return 80*cos(2*y)/(x*x+y*y+0.001)-50
def f5(x,y): return 5*sin(x*(y+4))*y
def f6(x,y): return -y*y/(x*x+0.001)

def eff(): fill_rect(0,0,320,240,(0,)*3)
      
def go(f,xmax=4,ymax=4):
  eff()
  h,v = 160,80
  for i in range(-h,h):
    m,n = 0,220
    for j in range(-v,v):
      x = -xmax*i/h-xmax*j/v
      y = ymax*i/h-ymax*j/v
      if (x / xmax)**2 + (y / ymax)**2 <= 1:
        z = 110-j-f(x,y)
        if z >= m or z <= n:
          m = max(z,m)
          # lumiere ou ombre
          c = (255,)*3 if z < n else (68,)*3
          n = min(z,n)
          set_pixel(i+160,int(z),c)

for i in range(7):
 go(eval("f"+str(i)))