Playlist YouTube sur la NUMWORKS
Vous êtes de corvée pour découper la galette des rois ? Certaines personnes veulent despetites parts et d’autres des parts normales ? Pas de panique, votre NUMWORKS va vous aider !
Outils nécessaires
Une galette des rois, une NUMWORKS et une règle graduée
Exemple n°1
La galette fait 24cm de diamètre, 3 personnes veulent une part normale et 2 personnes des parts petites (c’est-à-dire la moitié d’une part normale)
Exécutez le programme puis var et galette :
>>> from galette import *
>>> galette(24,3,2))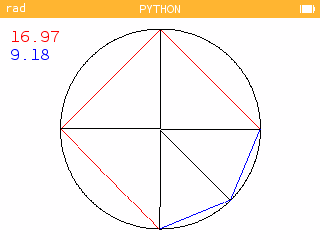
Mesurez 16.97 cm (disons 17 cm) trois fois, cela correspond aux 3 parts normales puis 9.18 cm (disons 9 cm) ce qui permet d’avoir les parts deux fois plus petites.
Exemple n°2
La galette fait 20cm de diamètre, 5 personnes veulent une part normale et 1 personne veut une part petite
Exécutez le programme puis var et galette :
>>> from galette import *
>>> galette(20,5,1))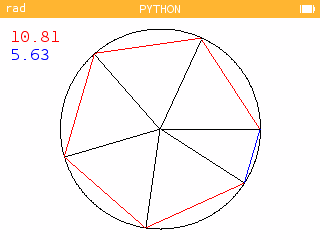
Mesurez 10.81 cm (disons 11 cm) cinq fois, cela correspond aux 5 parts normales, la part restant sera la petite.
Exemple n°3
La galette fait 18cm de diamètre, 3 personnes veulent une part normale
Exécutez le programme puis var et galette :
>>> from galette import *
>>> galette(18,3,0))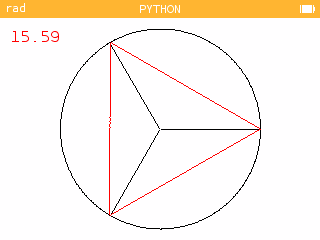
from math import * from kandinsky import * from turtle import * def line(x1, y1, x2, y2, coul): penup() goto(x1, y1) color(coul) pendown() goto(x2, y2) def galette(diam, normal, small): global a nb = 2 * normal + small penup() color((0, 0, 0)) goto(0, -100) pendown() circle(100) a = 0 a = affiche(2, nb, normal, (255, 0, 0)) a = affiche(1, nb, small, (0, 0, 255)) y1 = 10 if normal > 0: lnor = round(diam * sin(2 * pi / nb), 2) draw_string(str(lnor), 10, y1, (255, 0, 0)) y1 += 18 if small > 0: lsma = round(diam * sin(pi / nb), 2) draw_string(str(lsma), 10, y1, (0, 0, 255)) hideturtle() def affiche(c, nb, taille, coul): global a for i in range(taille): r = 2 * c * pi / nb x1 = 100 * cos(a) y1 = 100 * sin(a) line(0, 0, x1, y1, (0, 0, 0)) line(x1, y1, 100 * cos(a + r), 100 * sin(a + r), coul) a += r return a