But de nos automates: Reconnaitre un langage

• Alphabet Σ : par exemple constitué de 2 lettres {a, b}
  
• Mots créés à partir de l’alphabet Σ : par exemples aaa, ababab, bbaaa, etc.
  
• Un automate va être un ensemble d’états (cercles) et de transitions (flèches)
  
• Un état initial (pour nous il n’y en aura qu’un seul et ce sera toujours le cercle de numéro “0”) et un ou plusieurs états finaux (cercles doubles)
  
• Un mot est accepté lorsque l’on arrive dans un état final sinon il est rejeté.

Automate n°1

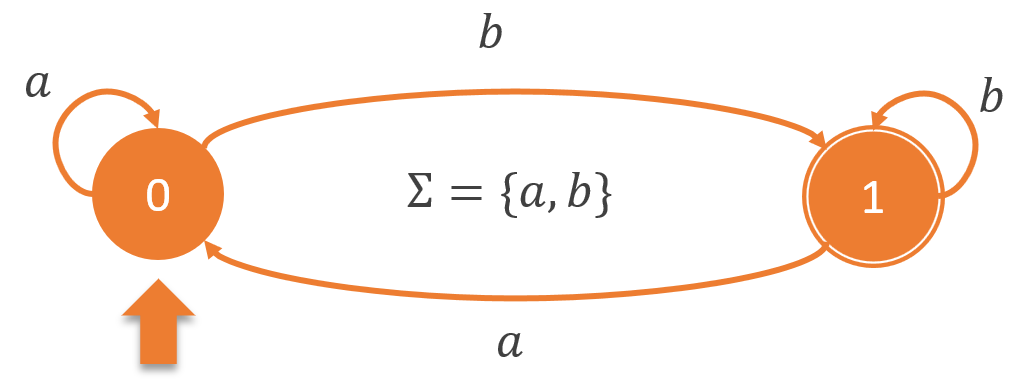
• Cet automate accepte-t-il le mot “ba” ? Réponse : NON, car en partant de l’état 0, la lettre “b” nous amène au cercle 1 puis le “a” nous ramène à l’état 0. Or cet état n’est pas un état final (pas de cercle double comme pour le 1). Donc le mot est refusé.
• Cet automate accepte-t-il le mot “abbb” ? Réponse : OUI, le “a” nous amène au cercle 1 puis on y reste avec les 3 “b”.
• Intuitivement, quels mots reconnait cet automate ? Réponse : Que l’on soit en 0 ou en 1, la lettre “a” nous ramène en 0. Pour arriver en 1 il faudra donc que la dernière lettre soit obligatoirement un “b”. Inversement, il suffit que le mot se termine par un “b” pour arriver à l’état final 1. Cet automate reconnait tous les mots (écrits avec l’alphabet Σ = {a, b} qui se terminent par “b”)

Automate n°2

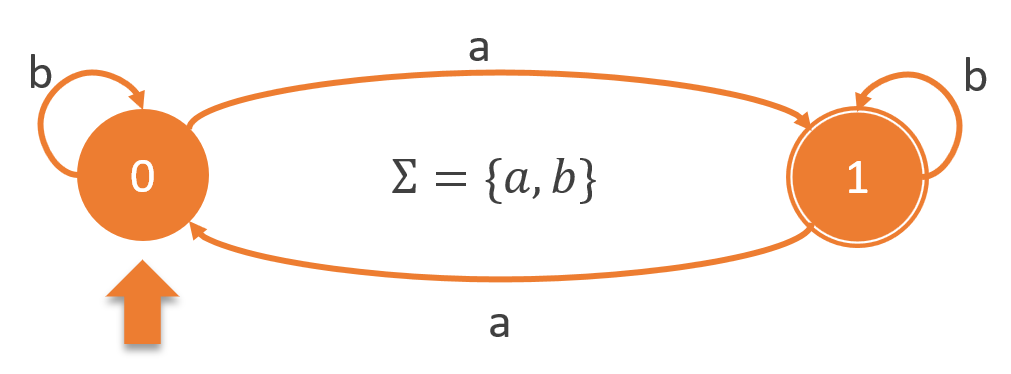
Il ressemble beaucoup au précédent mais il ne reconnait pas du tout le même langage !

• Cet automate accepte-t-il le mot “ba” ? Réponse : OUI
• Cet automate accepte-t-il le mot “aa” ? Réponse : NON
• Cet automate accepte-t-il le mot “abbaabb” ? Réponse : OUI
• Intuitivement, quels mots reconnait cet automate ? Réponse : Les mots qui contiennent un nombre impair de “a”
  

On re

a1 = [{"a":0,"b":1},{"a":0,"b":1}]
f1 = [1]

a2 = [{"a":1,"b":0},{"a":0,"b":1}]
f2 = [1]

def accepte(mot,a,f):
    e = 0
    for c in mot:
        e = a[e][c]
    return e in f
        
# accepte("abbb",a1,f1) donne True 
# accepte("abbaabb",a2,f2) donne True

def details(mot,a,f):
    e = 0
    for c in mot:
      print("Etat "+ str(e))
      e = a[e][c]
      print("Lettre "+c+" >")
    if e in f:
      return str(e)+ " = etat final"
    return str(e)+" = pas final"